Postingan
BAB 2. KONSEP-KONSEP DASAR
2.1 Jika ν = 141.4 sin (ωt + 30°)V dan I = 11.31 cos (ωt - 30°)A, hitunglah untuk masing-masing (a) nilai maksimum, (b) nilai rms, dan (c) rumus phasor dalam bentuk polar dan rectangular dengan memilih tegangan sebagai dasar. Apakah rangkaian itu induktif atau kapasitif ?
Jawab :
a) Vmax = 141.4 V
I max = 11.31 A
b)
c) V = 100‚0° V (phasor) = 100 + j 0 V (polar)
I = 8‚-60° A (phasor) = 4 – j 6.93 A (polar) ==> Induktif, I tertinggal tehadap V.
2.2 Jika rangkaian pada soal 2.1 terdiri dari suatu elemen resistif murni dan suatu elemen reaktif murni, hitunglah R dan X (a) Jika elemen-elemen terhubung seri dan (b) Jika elemen-elemen terhubung paralel.
Jawab :
a)
a)
Z = 6.25 + j 10.83 Ω ; ==> R = 6.25 Ω, dan XL = 10.83 Ω
b) Y = 1/Z = 0.08‚-60° = 0.04 – j 0.0693
R = 1/0.04 = 25 Ω, dan XL = 1/0.0693 = 14.43 Ω
2.3 Dalam suatu rangkaian berfasa-tunggal Va = 120‚45° V dan Vb = 100‚-15° V terhadap suatu simpul pedoman o. Carilah Vba dalam bentuk polar.
Jawab :
Vba = Vbo – Vao = 100 ‚-15° - 120‚ 45°
Vba = 96.59 – j 25.88 – (84.85 + j 84.85) = 96.59 – 84.85 – j 25.88 – j 84.85
Vba = 11.74 – j 110.73 = 111.35‚ - 83.95° V
2.4 Suatu tegangan ac berfasa tunggal sebesar 240 V terpasang pada suatu rangkaian seri yang impedansinya adalah 10‚60° Ω. Hitunglah R, X, P, Q dan factor daya dari rangkaian.
Jawab :
R = 10 Cos 60° = 5.0 Ω, X = 10 Sin 60° = 8.66 Ω
I = 240‚ 0°/ 10 ‚ 60° = 24‚-60° A
P = (24)2 x 5 = 2880 W
Q = (24)2 x 8.66 = 4988 Var
Faktor daya = Cos (arc tg Q/P ) = Cos (arc tg 4988/2880) = 0.50
Atau Cos (arc tg X/R ) = Cos (arc tg 8.66/5 ) = 0.50
2.5 Jika suatu kapasitor dihubungkan paralel dengan rangkaian pada soal 2.4 dan jika kapasitor ini mencatu 1250 Var, hitunglah P dan Q yang dicatu oleh sumber tegangan 240 V, dan hitunglah faktor daya yang dihasilkannya.
Jawab :
P = 2880 W ; Q = 4988 – 1250 = 3738 Var;
Faktor daya = Cos (arc tg 3788/2880 ) = 0.605
2.6 Suatu beban induktif berfasa-tunggal menarik 10 MW dengan faktor daya 0.6 tertinggal. Gambar lah segitiga daya dan tentukan daya reaktif dari sebuah kapasitor yang harus dihubungkan paralel dengan beban untuk menaikkan faktor daya menjadi 0.85.
Jawab :
Faktor daya awal = Cos φ1 = 0.6 jadi φ1 = arc Cos 0.6 = 53.13°
sehingga Sin φ1 = Sin 53.13° = 0.8
sehingga Sin φ1 = Sin 53.13° = 0.8
P = VI Cos φ1 ; 10 = VI . 0.6 ==> jadi VI = 10/0.6
Q1 = VI Sin φ1
Q1 = (10/0.6) x 0.8 = 13.33 Mvar
Faktor daya baru = Cos φ2 = 0.85 jadi φ2 = arc Cos 0.85 = 31.79°
sehingga Sin φ2 = Sin 31.79° = 0.53
sehingga Sin φ2 = Sin 31.79° = 0.53
P = VI Cos φ2; 10 = VI 0.85 ==> jadi VI = 10/0.85
Q2 = VI Sin φ2
Q2 = (10/0.85) x 0.53 = 6.2 Mvar
Jadi QC = - ( 13.33 – 6.2) = - 7.13 MVar
2.7 Sebuah motor induksi berfasa-tunggal beroperasi dengan beban yang sangat ringan untuk sebagian besar dari tiap-tiap hari dan menarik 10 A dari saluran. Disarankan penggunaan suatu alat untuk “meningkatkan efisiensi” dari motor itu. Dalam suatu peragaan alat tersebut dihubungkan paralel dengan motor yang tidak dibebani dan arus yang ditarik dari saluran turun menjadi 8 A. Jika dihubungkan dua buah dari alat tersebut paralel dengan motor, arus yang ditarik turun lagi menjadi 6 A. Alat sederhana apakah yang menyebabkan penurunan arus ini ? Sebutkanlah keuntungan-keuntungan dari alat ini. Apakah alat ini juga menaikkan efisiensi dari motor ? (Ingatlah bahwa suatu motor induksi menarik arus yang tertinggal atau lagging).
Jawab :
Alat itu adalah Kapasitor; sebuah kapasitor akan menyebabkan jatuhnya arus pada saluran karena komponen yang tertinggal dari arus yang ditarik oleh motor sebagian akan diimbangi oleh arus yang mendahului yang ditarik oleh kapasitor. Tetapi arus yang ditarik oleh motor tidak akan berubah jika tegangan terminal tetap konstan. Jadi efisiensi motor akan tetap sama.
Rugi pada saluran yang mencatu motor akan berkurang, karena arus saluran menjadi rendah. Jika saluran dari bus catu ke motor adalah panjang, jatuh tegangan pada saluran akan berkurang dan ini mungkin dikehendaki.
2.8 Jika impedansi antara mesin-mesin 1 dan 2 pada Contoh 2.1 adalah Z = 0 – j5 Ω tentukanlah (a) apakah maisng-masing mesin membangkitkan atau menyerap daya, (b) apakah masing-masimg mesin menerima atau mencatu daya reaktor positif dan berapa besarnya, dan (c) nilai dari P dan Q yang diserap oleh impedansi tersebut.
Jawab :
I = 10 + j 2.68 ==> I = 10.35‚15° A
I = 10 + j 2.68 ==> I = 10.35‚15° A
E1. I* = (100 + j 0 )( 10 – j 2.68) = 1000 – j 268
Mesin 1 membangkitkan 1000 W, menerima 268 Var (atau mencatu – 268 Var)
E2 . I* = (86.6 + j 50) (10 – j 2.68) = 866 – j 232.088 + j 500 + 134 = 1000 + j 268
Mesin 2 menyerap 1000 W , menerima 268 Var ( atau mencatu – 268 Var)
Daya reaktansi pada saluran mencatu |I |2 X = (10.35)2 x 5 = 568 Var
(atau menerima - 568 Var)
(atau menerima - 568 Var)
2.9 Ulangi soal 2.8 di atas jika Z = 5 + j 0
Jawab :
I = 2.68 - j 10 ==> I = 10.35‚ -75° A
E1. I* = (100 + j 0 )( 2.68 + j 10) = 268 + j 1000
Mesin 1 membangkitkan 268 W, menyerahkan 1000 Var (atau mencatu – 268 Var)
E2 . I* = (86.6 + j 50) (2.68 + j 10) = 232 + j 866 + j 134 - 500 = - 268 +j 1000
Mesin2 membangkitkan 268 W, menerima 1000 Var (atau mencatu – 268 Var)
Daya resistansi pada saluran menyerap |I |2 R = (10.35)2 x 5 = 568 W
Kedua mesin adalah Generator
2.10 Suatu sumber tegangan Ean = - 120‚210° V dan arus yang mengalir lewat sumber tersebut adalah Ina = 10‚60° A. Carilah nilai-nilai dari P dan Q dan jelaskan apakah sumber tersebut memberikan atau menerimanya.
Jawab :
Ean . Ina* = - 120‚210° x 10‚-60° = |-120|.|10| ‚(210°-60°) = -1200‚150°
= 1200‚-30° = 1200.Cos -30° + j 1200.Sin -30° = 1039 – j 600
P = 1039 W diserahkan; Q = - 600 Var diserahkan
(+ 600 Var diserap oleh sumber, karena Ina mendifinisikan arus positif dari n ke a dan Eanmendifinisikan titk a pada potensial yang lebih tinggi daripada n bila Ean adalah positif).
2.11 Carilah jawaban dari Contoh 2.1 jika E1 = 100‚0° V dan E2 = 120‚30° V. Bandingkanlah hasilnya dengan Contoh 2.1 dan buatlah beberapa kesimpulan tentang pengaruh perubahan besarnya E2 dalam rangkaian itu.
Jawab :
I = - 12 + j 0.78
E1.I* = (100 + j 0)(-12 - j 0.78) = -1200 – j 78
Mesin 1 menyerap 1200 W dan menyerap 78 Var.
E2.I* = (103.92 + j 60)(-12 – j 0.78) = 1246.8 – j81.42 – j 720 + 46.8 = -1200 – j 801.42
Mesin 2 menyerahkan 1200 W dan menyerahkan 801Var
yang diserap oleh saluran = 801 – 78 = 723 Var. Dalam contoh 2.1 saluran menerima 536 Var, setengah masing-masing sumber. Peningkatan |E2| menyebabkan sedikit kenaikan pada transfer daya serta kenaikan pada Q yang dicatu ke saluran, tetapi fakta yang penting ialah bahwa peningkatan |E2| mennyebabkan bahwa sumber tidak hanya mencatu Q yang diserap oleh saluran tetapi juga 78 Var yang diserahkan ke sumber |E1|.
2.12 Tiga buah impedansi yang identik yaitu 10 ‚-15° Ω dihubungkan Y kepada tegangan-tegangan saluran tiga-fasa yang seimbang dari 208 V. Tentukanlah semua tegangan-tegangan saluran, tegangan-tegangan fasa dan arus-arus sebagai phasor dalam bentuk polar dengan Vca sebagai pedoman dan urutan fasa abc.
Jawab :
Vca = 208‚0° V Vcn = 120‚-30° V Ic = Vcn/Z = 12‚-15°
Vbc = 208‚120° V Vbn = 120‚ 90° V Ib =Vbn/Z = 12‚105°
Vab = 208‚240° V Van = 120‚210° V Ia =Van/Z = 12‚225°
2.13 Dalam suatu sistem tiga-fasa yang seimbang, impedansi yang dihubungkan Y adalah 10‚- 30° Ω. Jika Vbc = 416‚90° V, tentukanlah Icn dalam bentuk polar.
Jawab:
Vbc = 416‚90° V ==> Tegangan fasa = 416/√3 = 240 V
Vcn = 240‚-60° ==> Icn =(240‚-60° )/( 10‚- 30°) = 24‚- 90° A
2.14 Terminal-terminal dari suatu sumber tiga-fasa ditandai dengan a, b, dan c. Di antara dua terminal yang mana pun sebuah voltmeter mengukur 115 V. Sebuah tahanan 100 Ω dan sebuah kapasitor 100 Ω (pada frekuensi sumber tegangan) dihubungkan seri dari a ke b dengan tahanan terhubung pada a. Titik hubung antara kedua elemen tersebut ditandai n. Tentukanlah secara grafik pembacaan voltmeter antara c dan n jika urutan fasa adalah abc dan jika urutan fasa acb.
Jawab :
Urutan fasa abc : Urutan fasa acb :
Jarak : n – k = 115/2 = 57.5 V Jarak : k – c = 99.6 V
Jarak : k – c = 115 Sin 60° Jarak : n – k = 57.5 V
= 115 x 0.866 = 99.6 V Jarak : n – c = 99.6 – 57.5 = 42.1 V
Pembacaan meter = 57.5 + 99.6 = 157.1 V Pembacaan meter = 42.1 V
2.15 Tentukanlah arus yang ditarik dari saluran 440 V tiga-fasa oleh sebuah motor tiga-fasa 15 hp yang beroperasi pada beban penuh, efisiensi 90 % dan faktor daya 80 % tertinggal. Hitunglah nilai-nilai dari P dan Q yang ditarik dari saluran.
Jawab :
di tarik dari saluran
2.16 Jika ketiga saluran yang menghubungkan motor pada soal 2.15 ke suatu bus masing-masing mempunyai imepansi 0.3 + j 1.0 Ω, hitunglah tegangan antar saluran pada bus yang mencatu 440 V pada motor.
Jawab :
I = | I | ( Cos φ – j Sin φ ) = 20.39 (0.8 – j 0.6) = 16.31 – j 12.23 A
Bila sebagai pedoman diambil tegangan ke netral dari motor pada terminal di mana I dihitung,
atau = 440/√3 = 254‚0° V = ( 254 + j 0) V,
maka tegangan bus catu ke netral adalah
Vn + (Z x I) = (254 + j 0) + (0.3 + j 1.0) (16.31 – j 12.23)
= 254 + j 0 + 4.893 – j 3.669 + j 16.31 + 12.23
atau = 440/√3 = 254‚0° V = ( 254 + j 0) V,
maka tegangan bus catu ke netral adalah
Vn + (Z x I) = (254 + j 0) + (0.3 + j 1.0) (16.31 – j 12.23)
= 254 + j 0 + 4.893 – j 3.669 + j 16.31 + 12.23
= 271.123 + j 12.641 = 271.4‚2.67°
Tegangan antar saluran | V | = √3 [271.123 + j 12.641] = √3 x 271.4= 470 V
2.17 Suatu beban Δ seimbang yang terdiri dari tahanan-tahanan murni sebesar 15 Ω per fasa dihubungkan paralel dengan suatu beban Y seimbang yang mempunyai impedansi-impedansi fasa 8 + j 6 Ω. Ketiga saluran yang menghubungkan kombinasi beban-beban tersebut di atas ke sesuatu sumber tiga fasa 110 V mempunyai impedansi-impedansi identik yaitu masing-masing 2 + j 5 Ω. Hitunglah arus total dan faktor daya resultan.
Jawab :
sehingga mempunyai impedansi total pada beban:
= 3.49 ‚12.09° Ω = 3.41 + j 0.73Ω
Pada catu daya mempunyai impedansi total
Z = (2 + j 5) + (3.41 + j 0.73) = 5.41 + j 5.73 = 7.88‚46.65° Ω
Z = (2 + j 5) + (3.41 + j 0.73) = 5.41 + j 5.73 = 7.88‚46.65° Ω
Pada beban Vℓ = 8.06 x 3.49 = 28.13 V ke netral.
Tegangan saluran-saluran
2.18 Suatu beban tiga-fasa menarik 250 kW dengan faktor daya 0.707 tertinggal dari saluran 440 V. Paralel dengan beban ini terpasang sebuah kumpulan kapasitor yang menarik 60 kVar. Hitunglah arus total dan faktor daya resultan.
Jawab :
Faktor daya = Cos φ = 0.707 ==> φ = 45°
S1 = 250 + j 250
S2 = 0 - j 60
Daya total S = S1 + S2 = 250 + j 190 = 314 ‚37.23° kVA
Arus total | I | = 314000/(√3x440)= 412 A ; Faktor daya = Cos 37.23° = 0.796 tertinggal.
2.19 Sebuah motor tiga-fasa menarik 20 kVA dengan faktor daya 0.707 dari sebuah sumber 220 V. Tentukanlah rating kilovoltampere dari kapasitor-kapasitor untuk membuat faktor daya kombinasi menjadi 0.90 tertinggal, dan tentukanlah juga arus saluran sebelum dan sesudah penambahan kapasitor.
Jawab :
Rating kapasitor = y – y2 = 14.14 – 6.85 = 7.29 kVar
Sebelum penambahan kapasitor
2.20 Sebuah mesin “ drag line “ pada suatu tambang batu bara “open-pit” mempergunakan 0.92 MVA dengan faktor daya 0.8 tertinggal pada waktu mesin menggali batu bara. Pada waktu sekop-sekop mesin yang sudah terisi meninggalkan dinding tambang, mesin itu membangkitan (memberikan kepada sistem listrik), 0.10 MVA dengan faktor daya 0.5 mendahului. Pada akhir perioda penggalian perubahan besarnya arus dapat menyebabkan bekerjanya rele-rele pengaman yang terbuat dari rangkaian-rangkaian solid state. Karena itu perubahan besarnya arus perlu dibuat seminimal mungkin. Pertimbangkanlah penempatan kapasitor-kapasitor pada terminal-terminal mesin dan tentukanlah besarnya koreksi kapasitif (dalam kVar) yang diperlukan untuk menghilangkan perubahan besarnya arus keadaan-tetap. Mesin itu mendapat tenaga dari sumber 36.5 kV tiga-fasa. Mulailah jawaban dengan memisalkan Q sebagai megavars total tiga-fasa dari kapasitor-kapasitor yang dihubungkan pada terminal-terminal mesin dan tuliskan rumus-rumus untuk besarnya arus saluran yang ditarik oleh mesin dengan Q sebagai faktor-faktornya baik untuk operasi “penggalian” maupun “pembangkitan”.
Jawab :
Misalkan tegangan antar saluran | V | adalah konstan. Maka besar arus | I | konstan,
berarti | S | konstan, dimana | S | = |V|.|I*| x 10- 6 MVA
Perioda penggalian :
Faktor daya = cos φ = 0.8 ; ==> sin φ = 0.6
|S| = | VI (cos φ + j sin φ) – j Q|
|S| = | 0.92(0.8 + j 0.6) – j Q| = | 0.736 + j 0.552 – j Q| = |0.736 + j (0.552-Q)|
|S|2= | 0.736 + j (0.552 – Q) |2
|S|2= 0.542 + (0.552-Q)2 = 0.542 + 0.3047 – 1.104 Q + Q2 = 0.8467 – 1.104Q + Q2
|S|2= 0.8467 – 1.104Q + Q2
Perioda pembangkitan :
Faktor daya = cosφ = 0.6; ==> φ = cos-1 0.6 = 60°
|S| = | - (0.10 ‚-60° ) - j Q| = | - ( 0.05 – j 0.0866) – j Q| = | - 0.05 + j 0.0866 – j Q |
|S|2= | - 0.05 + j (0.0866 – Q)|2
|S|2= 0.0025 + (0.0866 – Q)2 = 0.0025 + 0.0074995 – 0.1732Q + Q2
|S|2= 0.0099995- 0.1732Q + Q2
|S|2= 0.0099995- 0.1732Q + Q2
|S|2= 0.01 – 0.1732Q + Q2
Dengan menyamakan |S|2 untuk perioda-perioda penggalian dan pembangkitan sehingga diperoleh :
0.8467 – 1.104Q + Q2 = 0.01 – 0.1732Q + Q2
0.8367 – 0.9308Q = 0
Maka Q = 0.8367/0.9308 = 0.8989 ≈ 0.899 Mvar atau 899 kVar.
2.21 Sebuah generator (yang dapat digambarkan sebagai suatu emf yang terhubung seri dengan sebuah reaktansi induktif) mempunyai rating 500 MVA, 22 kV. Kumparan-kumparannya yang terhubung Y mempunyai reaktansi 1.1 per unit. Hitunglah nilai ohm dari reaktansi kumparan-kumparannya.
Jawab :
2.22 Generator pada soal 2.21 berada dalam suatu rangkaian di mana dasar-dasarnya ditetapkan sebagai 100 MVA, 20 kV. Bertolak dari nilai per unit yang diberikan dalam soal 2.21, tentukanlah nilai per unit dari reaktansi kumparan-kumparan dengan dasar yang tersebut di atas.
Jawab :
Reaktansi X = 1.065 Ω pada rating lama 500 MVA, 22 kV
Reaktansi X pada rating baru 100 MVA, 20 kV adalah :
X = 1.065 x(100/500) x(22/20)2 = 0.2577 p.u
2.23 Gambarkanlah rangkaian ekivalen fasa-tunggal untuk motor (suatu emf yang terhubung seri dengan reaktansi induktif Zm ) dan hubungannya kepada tegangan suplai yang dibicarakan dalm soal-soal 2.15 dan 2.16. Tunjukkanlah pada diagram nilai-nilai per-unit dari impedansi saluran dan tegangan pada terminal-terminal motor dengan 20 kVA, 440 V sebagai dasar. Kemudian dengan mempergunakan nilai-nilai per unit hitunglah tegangan suplai dalam per-unit dan akhirnya rubahlah nilai per-unit dari tegangan supali ke dalam volt.
Jawab :
Impedansi 0.3 + j 1.0 Ω ( dari soal 2.16)
R =0.3/9.68 = 0.031 p.u dan X =1.0/9.68 = 0.1033 p.u
I = 20.39 A ( dari soal 2.15)
I =20.39/26.24 = 0.777 p.u
Dari soal 2.15 faktor daya 80 % tertinggal. ==> Cos φ = 0.8; Sin φ = 0.6
V = 1.0 + 0.777 ( 0.8 – j 0.6 ) ( 0.031 + j 0.1033)
V = 1.0 + 0.777 ( 0.0248 + j 0.08264 – j 0.0186 + 0.061998 )
V = 1.0 + 0.777 ( 0.086798 + j 0.06404 ) = 1.0 + 0.0674 + j 0.0498
V = 1.0674 + j 0.0498
V = 1.0686 ‚2.67° p.u
| V | antar-saluran = 1.0686 x 440 ≈ 470 V
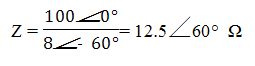
pada no 2.20 mengapa j^2 hasilnya menjadi positif?